Multi-Objective Search

This page summarizes my research on the multi-objective search problem. I also include the pointers to the papers and the code.

Overview

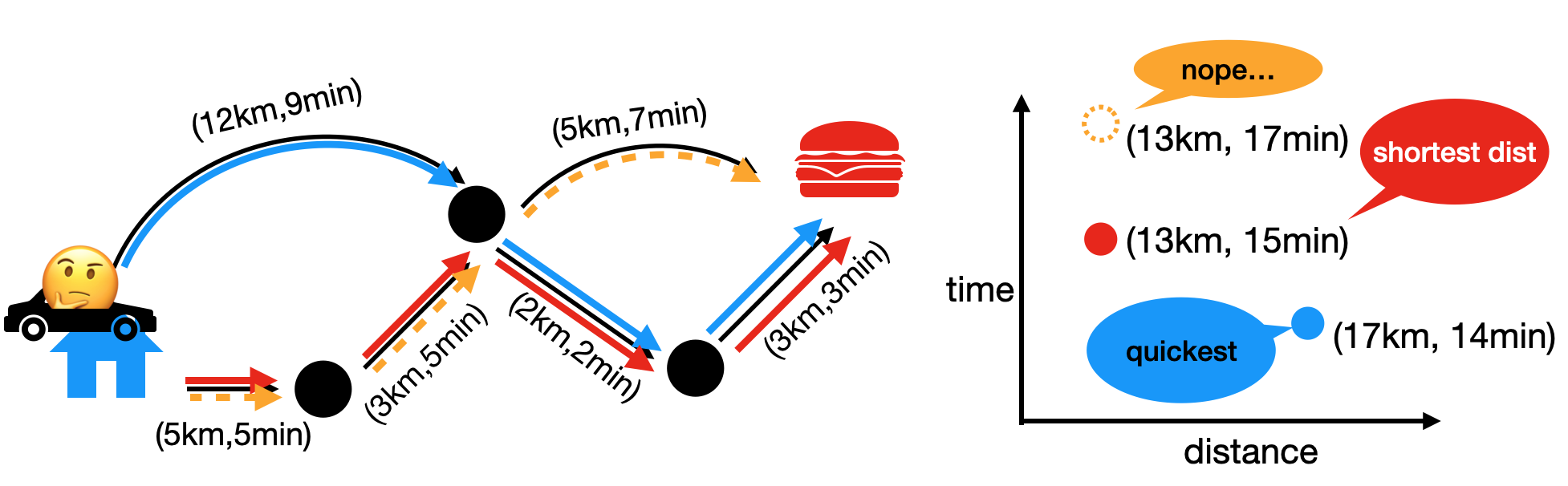
The multi-objective search problem is the problem of finding paths from a start state to a goal state in a graph where each edge is annotated with multiple costs. A typical task of multi-objective search is to find the Pareto frontier, that is, the set of all undominated paths from the start state to the goal state. This problem is important for many applications, such as transporting hazardous materials, where travel distance and risk are two costs that need to be considered.

The above figure shows an example problem of multi-objective search with two objectives, namely, travel distance and travel time. We need to find paths from home to the burger place. The Pareto frontier contains two paths: The red path has the smallest travel distance, and the blue path has the smallest travel time. Other paths, for example, the orange path, are dominated by either the red or the blue path.

My Ph.D. dissertation

While researchers have developed various techniques over the past years for speeding up single-objective searches on large graphs, many of them have not been investigated in the context of multi-objective search. In my dissertation, I hypothesize that one can speed up multi-objective search algorithms by applying insights gained from single-objective search algorithms after proper generalization. Specifically, I consider the following four classes of techniques that have been used to speed up single-objective search algorithms, namely, (1) by trading off solution quality with efficiency, (2) by anytime search, (3) by preprocessing techniques, and (4) by efficient data structures for time-consuming operations.

Code: https://github.com/HanZhang39/MultiObjectiveSearch.

Approximate search

We propose A*pex, an approximate multi-objective search algorithm that computes an \(\varepsilon\)-approximate Pareto frontier for a user-specified \(\varepsilon\)-value. We showed that an approximate Pareto frontier can be computed much faster than the Pareto frontier.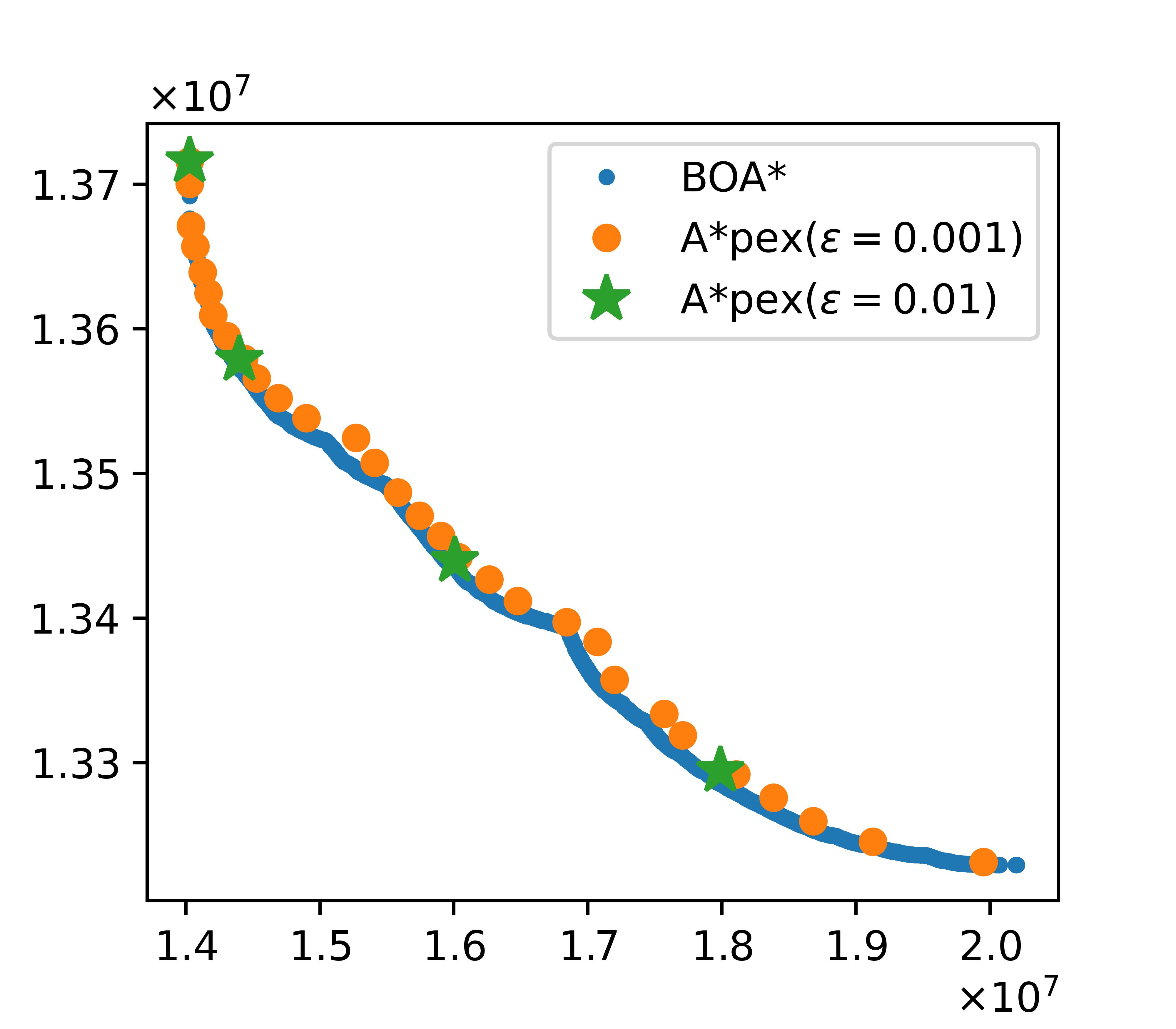

The Pareto frontier (9114 solutions), a 0.001-approximate Pareto frontier (30 solutions), and a 0.01-approximate Pareto frontier (4 solutions) computed by BOA*, A*pex with \(\varepsilon=0.001\), and A*pex with \( \varepsilon=0.01 \), respectively, for a road-network problem instance with two objectives. While it takes BOA* 170 seconds to compute the Pareto frontier, it takes A*pex, our proposed algorithm, only 15 seconds and 7 seconds to compute the approximate Pareto frontiers with \(\varepsilon = 0.001\) and \(\varepsilon = 0.01\), respectively.

Anytime search

We propose A-A*pex, an anytime approximate multi-objective search algorithm that quickly computes an approximate Pareto frontier and, while time allows, works on computing more solutions until it finds the Pareto frontier. Such an anytime algorithm could be useful if one only has a limited amount of runtime available for solving a multi-objective search problem instance.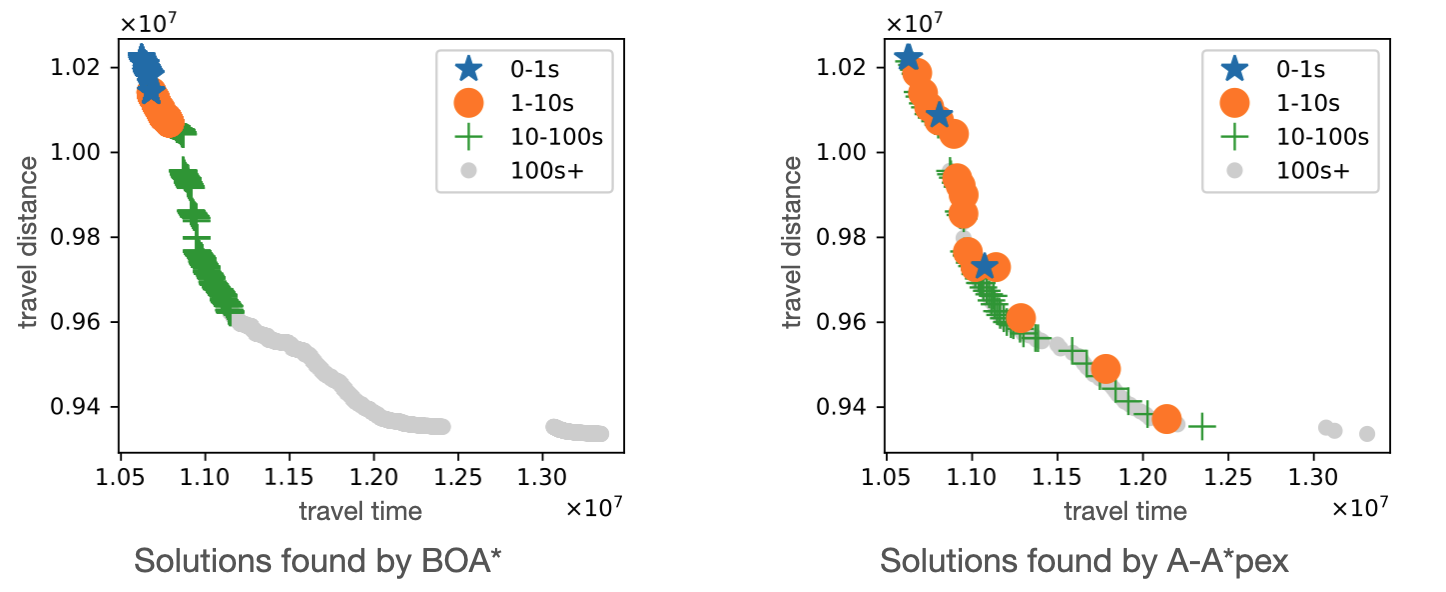

The solutions found by BOA* (existing algorithm) and A-A*pex (our proposed algorithm) for a bi-objective search problem instance on the FLA road network. Different markers indicate different time ranges when the solutions were found. If one is given a limited amount of time, for example, 1s, 10s, or 100s, running A-A*pex results in solutions that are much better distributed than those of the solutions found by BOA*.

Contraction hierarchies

In single-objective search, the contraction hierarchy is a speed-up technique for quickly computing the shortest path. We show that contraction hierarchies can be generalized to multi-objective search as well, resulting in orders-of-magnitude speed-up.

Data structures

For multi-objective search algorithms, dominance checks are often the most time-consuming operations. We propose the bucket array, a data structure for speeding up the dominance checks.

Other works

Aside from the works I included in the dissertation, I am also involved in the following works that are related to multi-objective search.

Optimal search algorithms

We have proposed several state-of-the-art multi-objective search algorithms for computing the Pareto frontier [1,2] and a theoretical analysis of node expansions in multi-objective search [3].

Related publications: [1] BOA* [2] LTMOA* [3] Must-expand nodes

Speed-up techniques

We have generalized differential heuristics (DHs), another speed-up technique for single-objective search, to the bi-objective search [1]. We have also proposed to speed up dominance checks via vectorized operations offered by Single Instruction/Multiple Data (SIMD) [2].

Related publications: [1] Bi-Objective DH [2] SIMD

Applications

We have applied the multi-objective search techniques to other problems, including the multi-objective multi-agent path finding problem [1,2,3], the weight-constrained shortest path problem [4], and the bounded-cost bi-objective search problem [5].

Related publications: [1] Cost-splitting for MO-CBS [2] BB-MO-CBS [3] BB-MO-CBS-pex [4] WCA*pex [5] Bounded-cost search

Survey

Heuristic-Search Approaches for the Multi-Objective Shortest-Path Problem: Progress and Research Opportunities

Han Zhang